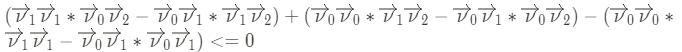后半部分的本来是LaTex公式,Hexo渲染有问题,尝试各种方法无果,暂时换成截图。
夹角的和
$\angle{APB}$+$\angle{BPC}$+$\angle{APC}$ = $2\pi$
方法较慢,且涉及到求反三角函数,直接淘汰。
面积法
已知道三角形的三点坐标,由海伦公式可以直接得到面积。

比较$S\triangle{APB} + S\triangle{BPC} + S\triangle{CPA}$ 和 $S\triangle{ABC}$是否相等即可,但是由于面积公式涉及开平方根,会产生浮点数的精度问题。当然面积也可以根据叉积大小来求。
同侧法
点 P 在$\triangle{ABC}$内部,则同时满足:
- 点 P 和 C 在直线 AB 的同侧,$\overrightarrow{AP}$ X $\overrightarrow{AB}$与$\overrightarrow{AC}$ X $\overrightarrow{AB}$方向相同
- 点 P 和 A 在直线 BC 的同侧,$\overrightarrow{BP}$ X $\overrightarrow{BC}$与$\overrightarrow{BA}$ X $\overrightarrow{BC}$方向相同
- 点 P 和 B 在直线 AC 的同侧,$\overrightarrow{AP}$ X $\overrightarrow{AC}$与$\overrightarrow{AB}$ X $\overrightarrow{AC}$方向相同
优化
三角形中,任意两条边的叉积大小为三角形的面积的两倍,方向由右手螺旋定则判断。
$\overrightarrow{AC}$ X $\overrightarrow{AB}$、$\overrightarrow{BA}$ X $\overrightarrow{BC}$、$\overrightarrow{AB}$ X $\overrightarrow{AC}$方向相同,只需判断$\overrightarrow{AP}$ X $\overrightarrow{AB}$、$\overrightarrow{BP}$ X $\overrightarrow{BC}$、$\overrightarrow{AP}$ X $\overrightarrow{AC}$、$\overrightarrow{AB}$ X $\overrightarrow{AC}$方向
再优化
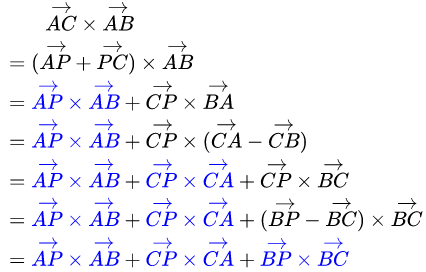
只需判断$\overrightarrow{AP}$ X $\overrightarrow{AB}$、$\overrightarrow{BP}$ X $\overrightarrow{BC}$、$\overrightarrow{AP}$ X $\overrightarrow{AC}$方向
重心法
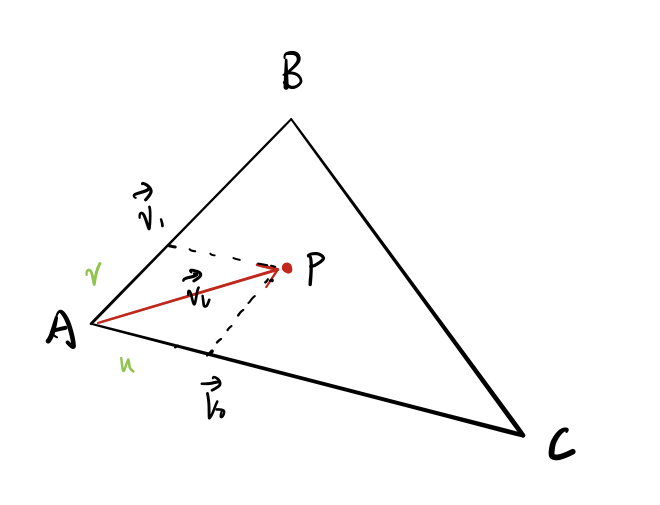
令$\overrightarrow{\nu_0}$=$\overrightarrow{AC}$,$\overrightarrow{\nu_1}$=$\overrightarrow{AC}$,$\overrightarrow{\nu_2}$=$\overrightarrow{AP}$,将$\overrightarrow{\nu_0}$、$\overrightarrow{\nu_1}$作为一组基底,令$\overrightarrow{\nu_2}$=u$\overrightarrow{\nu_0}$ + v$\overrightarrow{\nu_1}$。
点P在$\triangle{ABC}$内部(边上也算),必须要满足:
- u ≥ 0且v ≥ 0
- u + v ≤ 1(反推法,取 BC 上一点 p’= $\overrightarrow{\nu_0}$+λ($\overrightarrow{\nu_1}$-$\overrightarrow{\nu_0}$),那么 u=(1-λ)、v=λ,u+v=1)
解出u、v,有
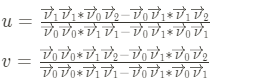
由柯西不等式的向量形式可以得到:

所以分母不会为负,只需要判断分子的正负:
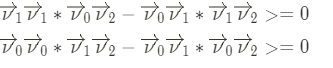
又需要满足u + v < 1,可以两边同乘以分母,避免了浮点数的除法运算: